![]()
Using congruence to establish a test for rhombuses
Theorem
A quadrilateral whose diagonals bisect each other at right angles is a rhombus.
Proof
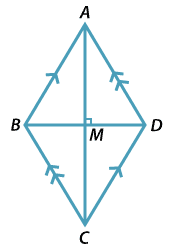
Let \(ABCD\) be a quadrilateral whose diagonals bisect each other at right angles at M.
We prove that \(DA = AB\). It follows similarly that
\(AB = BC\ \text{and} \ BC = CD\)
\(\triangle ABC \equiv \triangle CDA\) (AAS)
So \(AB = AD\) and by the first test above \(ABCD\) is a rhombus.




